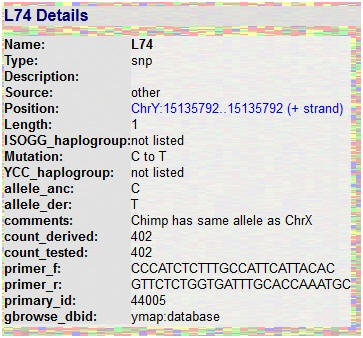
Kilka tysięcy praojców
            i tyleż pramatek mam.
Zapadły się ich mogiły
            i nie ma ich kości...
Ale znajduję coś w sobie
            - ich własne de-en-a.
Poznam je, przy nim uklęknę
            w synowskiej miłości!

      R1a1a1-M417*  i  H14a

Skąd pochodzą
 Polacy, Słowianie,
Europejczycy, inne ludy?

Dyskusja o mutacjach STR. Tablice

Ostatnia aktualizacja
tej strony

 07 maj 16
 

†

WYBIERZ RÓD:

PIETRZAKOWIE

JANIKOWIE .

SZLAGOWIE

KURCZABOWIE

nadto: GIERAŁTOWIE

GENEALOGIA GENETYCZNA.

Strony genealogii genetycznej na naszej witrynie

1. Genealogia Y i mtDNA, cz.1, haplogrupy R1a, R1b
 2. Geneza języków indoeuropejskich i początek Słowian
 3. Haplogrupy nieindoeuropejskie Y-DNA. Haplogrupy mitochondrialne mtDNA
    Jak zbadać swoje Y-DNA i mtDNA

Pochodzenie ludności w dorzeczu Dunajca i jego sąsiedztwie * Inne wybrane regiony

Ilustracje R1a1a: drzewa, mapy, filogeneza

Skąd, Europejczyku, jak i kiedy tu przybyłeś?

Nowiny i linki do naukowych publikacji

Rozmaitości genealogii genetycznej i dyskusja [cz.1] [cz.2]

Dyskusja o mutacjach STR. Faktyczny czas mutacji. TABLICE

Y-Adam, praojciec wszystkich współczesnych ludzi [1] [2] * Fundusz RRA00 [1] [2]
 Kreacjonizm ewolucjonistyczny   The evolutionistic creationism

Rejestr  zmian i aktualizacji
 

Uwaga. Stan dyskusji w latach 2010-2012, więc nieaktualny !!! (StP)
 

1. Mutacje STR i ich tempo w markerach

         W genealogii Y-DNA brane są pod uwagę mutacje w kilkudziesięciu szybkozmiennych miejscach DNA, zwanych markerami. Są to zmiany, polegające na wypadnięciu, dodaniu lub wymianie jednego z elementów powtarzającego się krótkiego tandemu (układu, sekwencji) zasad: A (adeniny), C (cytozyny), G (guaniny) i T (tiaminy). Na skutek takiej zmiany seria powtórzeń krótkiego tandemu (Short Tandem Repeats, STR) skraca się albo wydłuża. Liczba powtórzeń w danym miejscu (markerze) nazywana jest allelem.

         Zestaw kilkunastu lub kilkudziesięciu, np. 12, 24, 37 lub 67 alleli stanowi haplotyp Y-DNA danej osoby. O ile nie ma laboratoryjnie rozpoznanej mutacji SNP, wtedy właśnie liczba i rodzaj zaistniałych i przekazanych potomkom zmian, czyli mutacji w haplotypie, mogą stanowić narzędzie rozpoznania haplogrupy, czyli rodu genetycznego i obliczania czasu, jaki upłynął od wspólnego przodka kilku lub większej grupy osób. Dlatego ważna jest znajomość częstotliwości, czyli czasu powstawania owych mutacji.


1a. Tabela tempa mutacji w 67 markerach STR (wg FTDNA)
http://freepages.genealogy.rootsweb.ancestry.com/~geneticgenealogy/ratestuff.htm
(z przeliczeniem liczby mutacji w czasie 307125 lat w najbardziej powolnym DYS578 - stp.)

Years per Mutation @ 25 yrs/gen 

% of descendant haplotypes with at least 1 mutation after x years

Note: The 95% CI's for the mutation rates are appx -50% and +100%. This affects the following %'s accordingly.

# locus

rate

gen/mut

yr/mut

500 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

na  lat
307125

1 393 0.00076 1316 32895 2% 3% 6% 9% 12% 15% 18% 21% 24% 27% 30%

9,34
2 390 0.00311 322 8039 6% 12% 25% 37% 50% 62% 75% 87% 100% 112% 124%

38,20
3 19 0.00151 662 16556 3% 6% 12% 18% 24% 30% 36% 42% 48% 54% 60%

18,55
4 391 0.00265 377 9434 5% 11% 21% 32% 42% 53% 64% 74% 85% 95% 106%

32,56
5 385a 0.00226 442 11062 5% 9% 18% 27% 36% 45% 54% 63% 72% 81% 90%

27,76
6 385b 0.00226 442 11062 5% 9% 18% 27% 36% 45% 54% 63% 72% 81% 90%

27,76
7 426 0.00009 11111 277778 0% 0% 1% 1% 1% 2% 2% 3% 3% 3% 4%

1,11
8 388 0.00022 4545 113636 0% 1% 2% 3% 4% 4% 5% 6% 7% 8% 9%

2,70
9 439 0.00477 210 5241 10% 19% 38% 57% 76% 95% 114% 134% 153% 172% 191%

58,60
10 389i 0.00186 538 13441 4% 7% 15% 22% 30% 37% 45% 52% 60% 67% 74%

22,85
11 392 0.00052 1923 48077 1% 2% 4% 6% 8% 10% 12% 15% 17% 19% 21%

6,39
12 389ii 0.00242 413 10331 5% 10% 19% 29% 39% 48% 58% 68% 77% 87% 97%

29,73
13 458 0.00814 123 3071 16% 33% 65% 98% 130% 163% 195% 228% 260% 293% 326%

100,01
14 459a 0.00132 758 18939 3% 5% 11% 16% 21% 26% 32% 37% 42% 48% 53%

16,22
15 459b 0.00132 758 18939 3% 5% 11% 16% 21% 26% 32% 37% 42% 48% 53%

16,22
16 455 0.00016 6250 156250 0% 1% 1% 2% 3% 3% 4% 4% 5% 6% 6%

1,97
17 454 0.00016 6250 156250 0% 1% 1% 2% 3% 3% 4% 4% 5% 6% 6%

1,97
18 447 0.00264 379 9470 5% 11% 21% 32% 42% 53% 63% 74% 84% 95% 106%

32,43
19 437 0.00099 1010 25253 2% 4% 8% 12% 16% 20% 24% 28% 32% 36% 40%

12,16
20 448 0.00135 741 18519 3% 5% 11% 16% 22% 27% 32% 38% 43% 49% 54%

16,58
21 449 0.00838 119 2983 17% 34% 67% 101% 134% 168% 201% 235% 268% 302% 335%

102,96
22 464a 0.00566 177 4417 11% 23% 45% 68% 91% 113% 136% 158% 181% 204% 226%

69,53
23 464b 0.00566 177 4417 11% 23% 45% 68% 91% 113% 136% 158% 181% 204% 226%

69,53
24 464c 0.00566 177 4417 11% 23% 45% 68% 91% 113% 136% 158% 181% 204% 226%

69,53
25 464d 0.00566 177 4417 11% 23% 45% 68% 91% 113% 136% 158% 181% 204% 226%

69,53
Years per Mutation @ 25 yrs/gen 

% of descendant haplotypes with at least 1 mutation after x years

# locus rate gen/mut yr/mut 500 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000  
26 460 0.00402 249 6219 8% 16% 32% 48% 64% 80% 96% 113% 129% 145% 161%

49,38
27 H4 0.00208 481 12019 4% 8% 17% 25% 33% 42% 50% 58% 67% 75% 83%

25,55
28 YCAIIa 0.00123 813 20325 2% 5% 10% 15% 20% 25% 30% 34% 39% 44% 49%

15,11
29 YCAIIb 0.00123 813 20325 2% 5% 10% 15% 20% 25% 30% 34% 39% 44% 49%

15,11
30 456 0.00735 136 3401 15% 29% 59% 88% 118% 147% 176% 206% 235% 265% 294%

90,30
31 607 0.00411 243 6083 8% 16% 33% 49% 66% 82% 99% 115% 132% 148% 164%

50,49
32 576 0.01022 98 2446 20% 41% 82% 123% 164% 204% 245% 286% 327% 368% 409%

125,56
33 570 0.00790 127 3165 16% 32% 63% 95% 126% 158% 190% 221% 253% 284% 316%

97,04
34 CDYa 0.03531 28 708 71% 141% 282% 424% 565% 706% 847% 989% 1130% 1271% 1412%

433,79
35 CDYb 0.03531 28 708 71% 141% 282% 424% 565% 706% 847% 989% 1130% 1271% 1412%

433,79
36 442 0.00324 309 7716 6% 13% 26% 39% 52% 65% 78% 91% 104% 117% 130%

39,80
37 438 0.00055 1818 45455 1% 2% 4% 7% 9% 11% 13% 15% 18% 20% 22%

6,76
38 531 0.00037 2669 66724 1% 1% 3% 4% 6% 7% 9% 10% 12% 13% 15%

4,60
39 578 0.00008 12285 307125 0% 0% 1% 1% 1% 2% 2% 2% 3% 3% 3%

1,00
40 395s1 0.00031 3239 80982 1% 1% 2% 4% 5% 6% 7% 9% 10% 11% 12%

3,79
41 395s1 0.00031 3239 80982 1% 1% 2% 4% 5% 6% 7% 9% 10% 11% 12%

3,79
42 590 0.00054 1837 45916 1% 2% 4% 7% 9% 11% 13% 15% 17% 20% 22%

6,69
43 537 0.00057 1740 43508 1% 2% 5% 7% 9% 11% 14% 16% 18% 21% 23%

7,06
44 641 0.00018 5647 141171 0% 1% 1% 2% 3% 4% 4% 5% 6% 6% 7%

2,18
45 472 0.00001 67981 1699524 0% 0% 0% 0% 0% 0% 0% 0% 0% 1% 1%

-    

46 406s1 0.00154 651 16282 3% 6% 12% 18% 25% 31% 37% 43% 49% 55% 61%

18,86
47 511 0.00128 783 19581 3% 5% 10% 15% 20% 26% 31% 36% 41% 46% 51%

15,68
48 425 0.00018 5623 140584 0% 1% 1% 2% 3% 4% 4% 5% 6% 6% 7%

2,18
49 413 0.00202 494 12358 4% 8% 16% 24% 32% 40% 49% 57% 65% 73% 81%

24,85
50 413 0.00202 494 12358 4% 8% 16% 24% 32% 40% 49% 57% 65% 73% 81%

24,85
Years per Mutation @ 25 yrs/gen 

% of descendant haplotypes with at least 1 mutation after x years

# locus rate gen/mut yr/mut 500 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000  
51 557 0.00321 312 7796 6% 13% 26% 38% 51% 64% 77% 90% 103% 115% 128%

39,39
52 594 0.00029 3504 87602 1% 1% 2% 3% 5% 6% 7% 8% 9% 10% 11%

3,51
53 436 0.00018 5569 139237 0% 1% 1% 2% 3% 4% 4% 5% 6% 6% 7%

2,21
54 490 0.00019 5322 133049 0% 1% 2% 2% 3% 4% 5% 5% 6% 7% 8%

2,31
55 534 0.00832 120 3005 17% 33% 67% 100% 133% 166% 200% 233% 266% 299% 333%

102,20
56 450 0.00020 4903 122579 0% 1% 2% 2% 3% 4% 5% 6% 7% 7% 8%

2,51
57 444 0.00321 312 7793 6% 13% 26% 38% 51% 64% 77% 90% 103% 115% 128%

39,41
58 481 0.00544 184 4596 11% 22% 44% 65% 87% 109% 131% 152% 174% 196% 218%

66,82
59 520 0.00245 408 10188 5% 10% 20% 29% 39% 49% 59% 69% 79% 88% 98%

30,15
60 446 0.00365 274 6844 7% 15% 29% 44% 58% 73% 88% 102% 117% 132% 146%

44,88
61 617 0.00042 2363 59074 1% 2% 3% 5% 7% 8% 10% 12% 14% 15% 17%

5,20
62 568 0.00053 1901 47514 1% 2% 4% 6% 8% 11% 13% 15% 17% 19% 21%

6,46
63 487 0.00097 1032 25801 2% 4% 8% 12% 16% 19% 23% 27% 31% 35% 39%

11,90
64 572 0.00212 472 11795 4% 8% 17% 25% 34% 42% 51% 59% 68% 76% 85%

26,04
65 640 0.00034 2956 73901 1% 1% 3% 4% 5% 7% 8% 9% 11% 12% 14%

4,16
66 492 0.00042 2363 59074 1% 2% 3% 5% 7% 8% 10% 12% 14% 15% 17%

5,20
67 565 0.00087 1144 28610 2% 3% 7% 10% 14% 17% 21% 24% 28% 31% 35%

10,73
# locus rate gen/mut yr/mut 500 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000  

R A Z E M   M U T A C J I   W   H A P L O T Y P I E   67 - M A R K E R O W Y M

2755,48

 

1b. Tabela tempa mutacji w markerach 68-111 (wg FTDNA)

Na podstawie: S.Paterson, maj 2011  ( http://dl.dropbox.com/u/2733445/MODEL1.xlsx )

Zob. J.Chandler, w: RootsWeb, 27.06.2011 (z przeliczeniem ilości mutacji; stp.)

Tempo mutacji w markerach od 68-111

L

o

c

u

s

Marker
STR

Liczba
mutacji
na marker
na pokolenie
wg Paterson-Chandler

Ilość
mutacji
w markerze
w stosunku
do STR435

A

B

C

D

68

DYS710

0,01722

344,4

69

DYS485

0,00204

40,8

70

DYS632

0,00001

-

71

DYS495

0,00135

27,0

72

DYS540

0,00077

15,4

73

DYS714

0,00502

100,4

74

DYS716

0,00042

8,4

75

DYS717

0,00265

53,0

76

DYS505

0,00355

71,0

77

DYS556

0,00142

28,4

78

DYS549

0,00432

86,4

79

DYS589

0,00192

48,4

80

DYS522

0,00103

20,6

81

DYS494

0,00008

1,6

82

DYS533

0,00362

72,4

83

DYS636

0,00099

19,8

84

DYS575

0,00018

3,6

85

DYS638

0,00063

12,6

86

DYS462

0,00046

9,2

87

DYS452

0,00223

44,6

88

DYS445

0,00082

16,4

89

Y-GATA-A10

0,00278

55,6

90

DYS463

0,00095

19,0

91

DYS441

0,00238

47,6

92

Y-ggaatt
 -1B07

0,00081

16,2

93

DYS525

0,00121

24,2

94

DYS712

0,02194

438,8

95

DYS593

0,00022

4,4

96

DYS650

0,00662

132,4

97

DYS532

0,00259

51,8

98

DYS715

0,00364

72,8

99

DYS504

0,00414

82,8

100

DYS513

0,00275

55,0

101

DYS561

0,00198

39,6

102

DYS552

0,00253

50,6

103

DYS726

0,00010

2,0

104

DYS635

0,00373

74,6

105

DYS587

0,00097

19,4

106

DYS643

0,00180

36,0

107

DYS497

0,00093

18,6

108

DYS510

0,00298

59,6

109

DYS434

0.00018

3,6

110

DYS461

0,00210

42,0

111

DYS435

0,00005

1,0
 

Razem mutacji w markerach 68-111:

2373,0

1c. Stosowane stopy mutacji w poszczególnych haplotypach
(zwłaszcza w środowisku Rosyjskiej Akademii Genealogii DNA)

Rodzaj
(długość)
haplotypu

Liczba mutacji
na jeden marker
na 25 lat

Liczba mutacji
na cały haplotyp
na 25 lat

Liczba lat
na jedną
pełną mutację

12 markerów

0,00183

0,022

1136

25 markerów

0,00184

0,046

543

37 markerów

0,00243

0,090

278

67 markerów

0,00179

0,120

111

111 markerów

0,00150

0,165

150

         Stosowanie powyższych  stóp mutacji wymaga uzupełnienia danymi z tablicy tzw. mutacji zwrotnych (powtórnych w tym samym markerze), których ilość zależy od liczby liczby tzw. mutacji prostych. Tablica ta jednak uwzględnia nieznaczną część mutacji powtórnych i daje wyniki znacznie zaniżone (zob. w Dyskusji). Stąd zachodzi potrzeba innego systemu obliczania czasu mutacji.
 

2. Nowy sposób liczenia czasu mutacji STR

         Założeniem poniższej tablicy jest fakt, że obserwowane (widoczne) mutacje powstają w dowolnej kolejności markerów. Statystycznie, jako widoczne ujawniają się zasadniczo tylko mutacje pierwsze w danym markerze. Równocześnie w markerach już zmutowanych dochodzi do licznych mutacji powtórnych, stosownie do tempa mutacji w danym markerze. Mutacje nie są jednokierunkowe, lecz (co do liczby alleli w markerze) mogą być na równi "w górę" lub "w dół", więc jakby drepczą w miejscu; dlatego mutacje powtórne można statystycznie uważać za niewidoczne.
         Czas mutacji widocznych w haplotypie nie dodaje się w sposób prosty (jak to praktykują niektórzy genealodzy Y-DNA), czyli jeżeli pierwsza mutacja (stopa mutacji) powstanie np. w czasie około 111 lat, to nie oznacza, że trzy mutacje pojawią się około 333 lata. O opóźnianiu się kolejnych mutacji decyduje ilość już zmutowanych i niezmutowanych markerów w haplotypie  oraz równoczesne "namnażanie się" mutacji powtórnych, statystycznie niewidocznych.
         Dlatego Rosyjska Akademia DNA-Genealogii posługuje się podwójną tablicą: jedna dla obliczania czasu mutacji prostych, a druga - mutacji powtórnych ("zwrotnych"), ale niestety o stawkach zaniżonych. Inni ustalają tzw. współczynnik ewolucyjny, jeden, niedopasowany ani do czasu bliskiego (zawyżony), ani do czasów bardzo odległych (zaniżony).
 

3. Pełny czas mutacji STR.
Podręczna i praktyczna tabela PCM.

Full Times of Mutations STR.
 The practical table FTM

( ulepszono / improved / 10.08.2012 - stp.)

 Obliczanie pełnego czasu mutacji ( PCM )
Calculation of full-time of mutations ( FTM )
67-markerowy haplotyp STR

GD
from
MRCA

Czas widocznych mutacji

i jego wykładniczy mnożnik,
uzyskany z podstawy
1,06713 (1...66)

 Years from   MRCA
 Czas od
MRCA
około lat:

A

B

C

1

111 x 1,00

111

2

222 x 1,07

238

3

333 x 1,14

380

4

444 x 1,22

542

5

555 x 1,30

722

6

666 x 1,38

919

7

777 x 1,48

1 150

8

888 x 1,58

1 403

9

999 x 1,68

1 678

10

1 110 x 1,79

1 987

11

1 221 x 1,92

2 344

12

1 332 x 2,04

2 717

13

1 443 x 2,18

3 146

14

1 554 x 2,33

3 621

15

1 665 x 2,48

4 129

16

1 776 x 2,65

4 606

17

1 887 x 2,83

5 340

18

1 998 x 3,02

6 034

19

2 109 x 3,22

6 791

20

2 220 x 3,44

7 637

21

2 331 x 3,67

8 555

22

2 442 x 3,91

9 548

23

2 553 x 4,18

10 672

24

2 664 x 4,46

11 881

25

2 775 x 4,76

13 209

26

2 886 x 5,07

14 632

27

2 997 x 5,42

16 244

28

3 108 x 5,78

17 964

29

3 219 x 6,17

19 861

30

3 330 x 6,58

21 911

31

3 441 x 7,02

24 156

32

3 552 x 7,49

26 604

33

3 663 x 8,00

29 304

-    ciąg dalszy / continuation   -

GD
from
MRCA

Czas widocznych mutacji

i jego wykładniczy mnożnik,
uzyskany  z podstawy
1,06713 (1...66)

 Years from
MRCA
 Czas od
MRCA
około lat:

A

B

C

34

3 774 x 8,53

32 192

35

3 885 x 9,11

35 392

36

3 996 x 9,72

38 841

37

4 107 x 10,37

42 590

38

4 218 x 11,07

46 693

39

4 329 x 11,81

51 125

40

4 440 x 12,60

55 944

41

4 551 x 13,45

61 211

42

4 662 x 14,35

66 900

43

4 773 x 15,32

73 122

44

4 884 x 16,34

79 805

45

4 995 x 17,44

87 113

46

5 106 x 18,61

95 023

47

5 217 x 19,86

103 610

48

5 328 x 21,19

112 900

49

5 439 x 22,62

123 030

50

5 550 x 24,14

133 977

51

5 661 x 25,76

145 827

52

5 772 x 27,48

158 615

53

5 883 x 29,33

172 548

54

5 994 x 31,30

187 612

55

6 105 x 33,40

203 907

56

6 216 x 35,64

221 538

57

6 327 x 38,03

240 616

58

6 438 x 40,59

261 318

59

6 549 x 43,31

283 637

60

6 660 x 46,22

307 825

61

6 771 x 49,32

333 946

62

6 882 x 52,63

362 200

63

6 993 x 56,17

392 797

64

7 104 x 59,94

425 814

65

7 215 x 63,96

461 471

66

7 326 x 68,25

500 000

67

-

-

Uwaga. Obliczanie czasu wymaga umiejętności ustalania liczby mutacji
i genetycznego dystansu do najbliższego wspólnego przodka – MRCA

Attention.  Time calculation requires counting skills mutations
and genetic distance to the recent common ancestor - MRCA)

         Powyższą tabelę PCM dla 67 markerowego haplotypu można także stosować
- dla mutacji w haplotypie 25 markerowym, mnożąc je przez 2,65
- dla mutacji w haplotypie 37 markerowym, mnożąc je przez 1,50
- dla mutacji w haplotypie 111 markerowym, dzieląc je przez 1,75

         Uwaga
         Środkowa kolumna (B) tej tabeli służy tylko uzasadnieniu wyniku.
 

3a. Zasady powstania podręcznej i praktycznej tabeli
pełnego czasu mutacji ( PCM )

         Tabela PCM powstała na podstawie następujących czynników

         1. Podstawą obliczeń w tabeli jest statystycznie domiemana obecność jednej mutacji w najbardziej wolno mutującym markerze, DYS425 = 500000 lat, a tym samym i w pozostałych markerach tego haplotypu.

         (The basis of calculation in the table is statistically determined the presence of one mutation in the most slow mutating marker, DYS425 = 500,000 years, and thus, and other markers of this haplotype).

         2. Ciąg wykładniczy (geometryczny) mutacji widocznych jest oparty na fakcie, że w haplotypie, wraz z kurczeniem się od 67/1 do 1/67 miejsc jeszcze niezmutowanych, odwrotnie wzrasta od 1/67 do 67/1 ilość miejsc na mutacje powtórne, czyli statystycznie niewidoczne (na miejsce mutacji widocznych powstają niewidoczne).

          Według publikowanych zwłaszcza przez FTDNA (i J.Chandlera) tabel mutacji w parach ojciec-syn, do mutacji STR w najbardziej powolnym markerze DYS425 (z poprawką Klosowa) w 66 markerowym haplotypie (po zrezygnowaniu z jeszcze bardziej powolnego DYS472) dochodzi statystycznie co 500.000 lat. Tymczasem, biorąc pod uwagę obliczone z tabeli J. Chandlera tempo mutacji w haplotypie: jedna mutacja na około 111 lat, do statystycznego czasu zaistnienia tej mutacji DYS425, a tym samym i całego zestawu 66 mutacji widocznych, powstaje około 4505 mutacji.

         Tak więc w czasie 66 mutacji widocznych, dochodzi także, w markerach już zmutowanych, do bardzo licznych mutacji powtórnych, czyli 4439 statystycznie niewidocznych, odpowiednio opóźniających czas owych mutacji widocznych, w sumie około 68,25 razy. Mutacje widoczne spowalniają się, gdyż w ich miejsce powstają wtedy mutacje powtóre, czyli statystycznie niewidoczne.

          To spowolnianie tempa mutacji widocznych, spowodowane kurczeniem się dla nich miejsc dotąd niezmutowanych oraz nierównością tempa mutacji w poszczególnych markerach od jeden do około kilkadziesiąt lub kilkaset, trzeba dla cełów obliczeniowych wyrazić ciągiem wykładniczym. Dlatego, aby otrzymać pełny czas mutacji ( PCM ) dla każdej liczby mutacji w tym 67 minus 1 markerowym haplotypie, należy znaleźć iloraz ciągu wykładniczego, tj. “a” w funkcji wykładniczej a x (1...65). Tym ilorazem a jest uwidoczniona na tabeli PCM liczba 1,06713.

         Uwaga 

         Powyższa zasada obliczania pełnego czasu mutacji (PCM), uwzględniająca pełny zestaw mutacji widocznych i niewidocznych (powtórnych) -
         a) nie wymaga osobnych tablic na tzw. mutacje zwrotne (zob. w tablicach A.Klosowa);
        b) nie wymaga stosowania dla czasów "ewolucyjnych" (np. powyżej 10000 lat) dodatkowej tabeli 22-markerowego haplotypu z wybranych markerów powolnych (zob. tablica Klosowa);
         c) nie wymaga wreszcie tzw. ewolucyjnego "współczynnika Żywotovskyego" (0,000069 mutacji na marker na pokolenie), który przy zastosowaniu go do czasów bliskich, genealogicznych,  zawyżając rezultat niekiedy aż trzykrotnie, wywołuje wśród genealogów i genetyków tak wiele sprzeciwu i krytyki.

         Równocześnie tablica PCM stwarza możliwość obliczania czasu najstarszych haplogrup i populacji, praktycznie od początku współczesnego człowieka.
 

3b. Krzywa wykładnicza czasu mutacji widocznych
 The exponential curve of time visible mutations

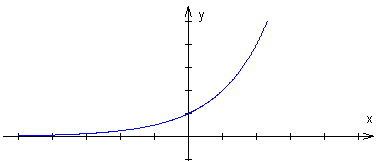
Wzrasta ogólna liczba mutacji i ich czas Y
ale zarazem spowolnia się i zatrzymuje przyrost mutacji widocznych X


 3c. Analogia - w krzywej wykładniczej czasu widocznych SNP
w/g modelu Jukesa-Cantora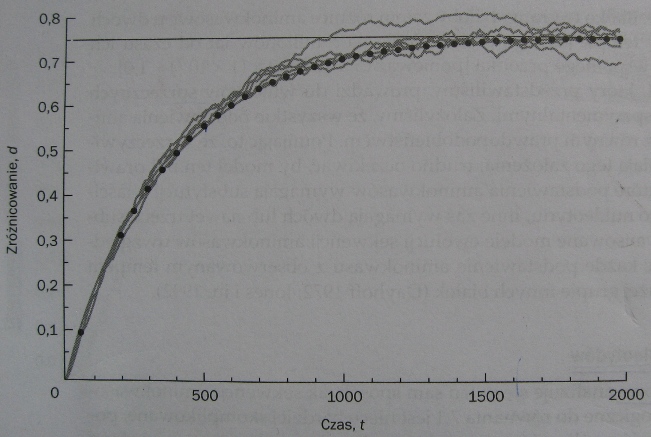

(Źródło wykresu: Podręcznik genetyki)

         Model Jukesa-Cantora (1969).  Model J-C  ilustruje fakt, że wraz ze wzrostem czasu t i ogólnej liczby mutacji ogranicza się, a w końcu całkowicie zatrzymuje się wzrost mutacji widocznych na rzecz niewidocznych, czyli widoczne zróżnicowanie d w badanym odcinku Y-DNA (NRY). Dalszemu  wzrostowi czasu nie odpowiada już żaden przyrost liczby mutacji widocznych.

         Dlatego nie ma sensu stosowanie liniowego liczenia czasu mutacji w haplotypie i stałego współczynnika czasu mutacji dla każdej widocznej mutacji, co niektórzy genetycy niestety praktykują.

...............................................................................................    ................................................................................
..............................................................................................     ................................................................................
 

4. Tabela 21 powolnych markerów
w haplotypie 67 markerowym

Table 21 slow markers  in 67-markers haplotype

(w 1. i 2. kolumnie wykorzystano markery i poprawki tempa ich mutacji od A. Klosowa)

Locus

mut./25 lat

mut./rok

czas 1 mut.
w latach

ilość mutacji
równoczesnych

DYS425

0,00005

0,0000020

500 000

1,00

DYS436

0,00006

0,0000024

416 667

1,12

DYS426

0,00009

0,0000036

277 778

1,80

DYS490

0,00013

0,0000050

200 000

2,50

DYS454

0,00016

0,0000064

156 250

3,20

DYS455

0,00016

0,0000064

156 250

3,20

DYS578

0,00017

0,0000068

147 059

3,40

DYS641

0,00017

0,0000068

147 059

3,40

DYS590

0,00017

0,0000068

147 059

3,40

DYS594

0,00020

0,0000080

125 000

4,00

DYS388

0,00022

0,0000088

113 636

4,40

DYS492

0,00023

0,0000092

108 696

4,60

DYS395Sb

0,00025

0,0000100

100 000

5,00

DYS450

0,00029

0,0000116

86 207

5,80

DYS617

0.00050

0,0000200

50 000

10,00

DYS531

0.00050

0,0000200

50 000

10,00

DYS640

0,00051

0,0000204

49 020

10,20

DYS392

0,00052

0,0000208

48 077

10,40

DYS568

0,00053

0,0000212

47 170

10,60

DYS395Sa

0,00053

0,0000212

47 170

10,60

DYS438

0.00055

0,0000220

45 454

11,00

Razem 120 mutacji  na 500.000 lat, tj. 1 mut. na 4167 lat

Uwaga.  Obliczanie czasu wymaga umiejętności liczenia mutacji
i genetycznego dystansu do najbliższego wspólnego przodka – MRCA.

Attention.  Time calculation requires counting skills mutations
and genetic distance to the nearest common ancestor – MRCA.

 

4a. Tabela 21 powolnych markerów
i ich pełny czas mutacji STR

w zakresie 67 markerowego haplotypu. Wykres wykładniczy.

Podstawą obliczeń w tabeli jest statystycznie określona obecność jednej mutacji w najbardziej wolno mutującym markerze, DYS425 = 500000 lat, a tym samym i w pozostałych markerach tego haplotypu..

Table of mutations time  in 21 slow markers
 in scope of 67-markers haplotype STR.  Exponential graph.

The basis of calculation in the table is statistically determined the presence of one mutation
in the most slow mutating marker, DYS425 = 500,000 years, and thus, and other markers of this haplotype.

 Obliczanie pełnego czasu mutacji ( PCM )
Calculation of full-time of mutations ( FTM )
21-markerowy haplotyp STR

GD od
MRCA
GD from
MRCA

Czas widocznych mutacji

i jego wykładniczy mnożnik,
uzyskany z podstawy
1,0910543 (1...20)

Lata od
MRCA
Years from
 MRCA

1

4167 x 1

4 167

2

8334 x 1,0911

9 093

3

12501 x 1,1904

14 881

4

16668 x 1,2988

21 648

5

20835 x 1,4171

29 525

6

25002 x 1,5461

38 656

7

29169 x 1,6869

49 205

8

33336 x 1,8405

61 355

9

37503 x 2,0080

75 306

10

41670 x 2,1909

91 295

11

45837 x 2,3904

109 569

12

50004 x 2,6080

130 410

13

54171 x 2,8455

154 144

14

58338 x 3,1046

181 116

15

62505 x 3,3873

211 723

16

66672 x 3,6957

246 400

17

70839 x 4,0322

285 637

18

75006 x 4,3993

329 974

19

79173 x 4,8000

380 030

20

83340 x 5,2370

436 452

21

87507 x 5,71383

500 000

Ulepszono / Improved / 10.08.2012,  Stanisław Pietrzak

.......................................................................................    ...............................................................................
.......................................................................................    ...............................................................................

5. Sposób liczenia mutacji w haplotypie,
genetycznego dystansu i czasu do najbliższego wspólnego przodka (TMRCA)

        
C. D. N.

 

6. Inny sposób obliczania czasu haplogrupy
- przy pomocy mutacji SNP

                 Powyższa tablica PCM haplotypu 67-markerowego ułatwia także, jak żadna inna, datowanie odległości czasowej od "chromosomalnego Adama" do dziś. Na przykład porównanie haplotypu Dorsey'a z haplogrupy A0 i haplotypów klanu Boyd z haplogrupy A1 daje wynik 55 GD do wspólnego przodka, Adama, czyli 136.000 lat.
         Natomiast porównanie dwóch dostępnych 67-markerowych haplotypów z haplogrupy A0 i losowo wybranych kilkudziesięciu haplotypów z całej gałęzi A1 i BT (z ludności afrykańskiej i pozaafrykańskiej) daje wynik 51,3, co wskazuje na czas 103.000 lat.

         (Na takie samo datowanie niespodziewanie wskazały świeżo opublikowane (maj 2012) wyniki dokładnych badań genealogii genetycznej i drzewa filogenetycznego ludzkich szczepów bakterii żołądkowej helikobakter pylori. Wynik identyczny jak powyższy: około 88.000-116.000 lat)    

         Potwierdzenie daje także moja pierwsza próba datowania Adama na podstawie liczby mutacji SNP. Mianowicie poniżej A* (Adam), czyli od haplogrup A1 do R włącznie, w ramach testowania w programie WTY, znajdujemy na dziś 63 mutacje typu SNP.

         W najdokładniej testowanej haplogrupie R1b od jej początku, czyli R-M343 do dzisiejszych ludzi, w kilku przykładowych gałęziach znajdujemy następujące liczby SNP:
L257=29, L1=28, L45=35, L148=35, Z343=34, M167=28, M228=30, Z35=30, L562=30, Z144=30, L705=29, L554=28, L362=29 i L658=31. Oznacza to, że poniżej R1 mamy średnio 30 (30,4) SNP.

T. Karafet haplogrupie R1 wyliczyła 18.500 lat, co oznacza 1 SNP na 617 lat.
A. Klosow zaś 23.000 lat, co oznacza 1 SNP na 767 lat.

Pod haplogrupą BT do dziś jest 117 SNP.
T. Karafet dla haplogrupy CT wylicza 70.000 lat, co oznacza 1 SNP na 598 lat.
A. Klosow zaś wylicza 64.000 lat, co oznacza 1 SNP na 547 lat.

W ten sposób u Karafet 1 SNP przypada średnio na 607 lat;
natomiast u Klosowa - na 657 lat.
Po uśrednieniu obydwu wyników - 1 SNP  na 630 lat.

To ułatwia datowanie haplogrupy A* (Adama, ojca A0 i A1):
163 SNP x 632 lata = 103.000 lat

         Wynik powyższy, obliczony tylko dla 163 SNP,  na pewno ulegnie zmianie po uwzględnieniu nowych mutacji STR i SNP niewielkiej grupy Pigmejów i Buszmenów (tzw. klan Perry'ego), której testowanie (z naszej inicjatywy i głównie naszymi nakładami finansowymi !) przeprowadzono w Stanach Zjednoczonych w FTDNA  i aktualnie (miesiące IV-VIII) trwa opracowywanie wyników na Uniwersytecie Arizona i Uniwersytecie Houston.

................................
UWAGA
      Po testach grupy Perry'ego, odkryciu i opublikowaniu kolejnych licznych mutacji SNP, ogólna ich liczba w genealogii najdokładniej przetestowanych próbek haplogrupy R1b wynosi około 203.
[Otwórz]
Oto nowe drzewo genealogiczne najstarszych haplogrup człowieka współczesnego.
Zmieniło się też datowanie MRCA, czyli pierwszego wspólnego przodka, ADAMA.
Żył on około 128.000 lat temu

 

 ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

         Nadto oczekujemy na nowe dane w sprawie czasu rozejścia się człowieka z istotami człekokształtnymi a także w sprawie tem,pa mutacji SNP w YDNA. Oto niektóre najnowsze dane w ważnej publikacji z 13 lipca 2012:
Generation times in wild chimpanzees and gorillas suggest earlier divergence times in great ape and human evolution, Kevin E. Langergraber et al. 2012.
http://email.eva.mpg.de/~paabo/pdf1/Langergraber_Generation_PNAS_doi.pdf

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

         Zobacz haplotypy Y-DNA haplogrupy A. Wymagają bardziej dokładnego testowania.
 http://www.familytreedna.com/public/African.DNAProject/default.aspx?section=yresults
http://www.familytreedna.com/public/Haplogroup_A/default.aspx?section=yresults

         Zob. polscy misjonarze wśród Pigmejów Batwa-Twa.
http://www.pigmeje.afrykadzika.com/videos/
         Czy Pigmejom wolno odmawiać godności "homo sapiens sapiens", jak to czynią niektórzy badacze?
 http://www.pigmeje.afrykadzika.com/videos/view.php?id=-D0xHsk4E8A&feature=youtube_gdata_player

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

6a. Pierwsza rozpoznana mutacja Adama,
ojca wszystkich ludzi: L74

Wyjaśnienie dra T. Krahna z genetycznego laboratorium Houston na RootsWeb
 So far all males are derived for L74.
I just noted and labeled L74 on the map because I noticed that the homologue
X chromosome sequence has a different allele at this position. So does the chimp Y chromosome.
Therefore L74 must have gotten derived after the human-chimp split.
It is likely that L74 is very old and most likely predates the molecular genetic Adam but we still need to confirm this with a hg A person.
Whenever the first reliable Neanderthal sequence is published I will
certainly check this marker against the data.
Else there is unfortunately not much to learn from it.
Thomas
 ................................
 When designing primers I oftentimes align the HUGO ChrY reference sequence to the Chimp ChrY reference sequence and to the human ChrX sequence.
This makes it easier to identify the ancestral and derived states of the SNPs and it makes sure that the primers that I design are located in a region that is selective for the Y chromosome but conservative enough to work for all human males (assuming that if the primers work even for chimps they should also work for all humans).
Because at the L74 location the X and chimp sequence had both a different base from the HUGO Y, I concluded that this position must have been derived after the human-chimp split.
No magic with molecular genetics, just common sense.
Thomas
 

         (Metoda obliczania TMRCA, stosowana zwłaszcza przez genetykę populacyjną, polega na wykorzystywaniu różnorodności, czyli sumy mutacji w całej grupie. Jest ona jednak bardzo mało wiarygodna, gdyż w dwóch grupach, powstałych w tym samym czasie i liczących np. po 100 osób, ilość mutacji może się bardzo różnić, w zależności od tego, kiedy grupa się rozrosła np. z kilku do stu osób. Jeśli wnet po powstaniu, czyli po TMRCA, to mutacji będzie bardzo dużo. Jeśli niedawno temu, to mutacji, przy tej samej liczbie osób, będzie bardzo mało. Ale genetyk, nieznający historii tej grupy, na podstawie niejednakowej różnorodności genetycznej, przypisze im bardzo różniące się czasy).

 

7. Dyskusje i uwagi

         Pouczające jest porównanie czasu  mutacji w standardowym, 67-markerowym haplotypie, według stawek mutacji i obliczeń czasu przez rosyjską Akademię Genealogii DNA A. Klosowa, z doliczonym czasem mutacji zwrotnych,oraz naszej tablicy tzw. pełnego czasu mutacji (PCM). Podane wyniki - w latach.

Liczba
mutacji		 Tablica
AG DNA		 Tablica
PCM / FMT

1
10
20
30
40
50
60
66

208
2.268
4.928
8.458
11.871
16.380
21.785
25.480

111
1.987
7.637
21.911
55.944
133.977
  307.825
  500.000

         Dlatego genealodzy rosyjscy (w osobie A. Klosowa),. widząc niesprawność swojej tablicy  obliczania czasu, na forum RootsWeb stwierdzają, że ich tablica ma przeznaczenie tylko do dystansu do około 15 tysięcy lat. Dla dalszego czasu radzą oni używać ich tabelę 22-markerową. Ta wykazuje jednak identyczne mankamenty, co poprzednia, tylko że na innym dystansie czasu.

         Zauważamy, że tabela PCM, uwzględniając rachubę wszystkich mutacji powtórnych (niewidocznych), które znacznie opóźniają pojawianie się bardziej licznych niż kilka-kilkanaście mutacji prostych (widocznych),  umożliwia datowanie haplotypów bardzo dawnych, sięgających Adama, przodka dzisiaj żyjących ludzi - około 142 tysiące lat (jak rachował Cruciani et al. 2011), a średnio i właściwie 103.000, jak tu rachujemy.

         W Y-DNA człowieka nie zauważamy więcej mutacji prostych względem MRCA niż 50 - 60, np. dla haplogrupy A (chromosomalny Adam). Reszta czasu zakodowana jest w ilości mutacji powtórnych (niewidocznych). Tabela PCM uwzględnia je i wprowadza w ogólną liczbę mutacji.

         Tablica PCM czyni zbędnymi starania  dla wypracowania "ewolucyjnego tempa mutacji", jak czyni Zhivotovsky dla starszych ponad 5000 lat haplotypów. Podobnie niepotrzebne jest tworzenie osobnej tablicy mutacji na podstawie 22 markerów powoli mutujących,  jak czyni AKlyosov dla obliczania czasu haplogrup i haplotypów sprzed 20000 lat, dokąd podstawowa tabela zasadniczo nie sięga. Na powyższym zestawieniu widać potrzebę owej dodatkowej tabeli  dla naprawienia olbrzymich rozbieżności między rezultatami podstawowej tabeli AK a faktycznym czasem mutacji.

         Uwaga. Nie ma sensu i jest zdecydowanie błędne rachowanie czasu według odległości genetycznej dwóch haplotypów (dwóch osób). Spotkane np. GD=100 między dwoma haplotypami należy najpierw podzielić przez dwa, aby uzyskać GD i czas wspólnego przodka MRCA.
         W ogóle problemem nadal do rozwiązania jest sposób liczenia liczby mutacji i dystansu genetycznego między dwoma haplotypami do współnego przodka.
 

 


E-mail: pietrzakstan@poczta.onet.pl

Wszelkie uwagi dla mnie proszę przekazać meilowemu gołąbkowi:

Dziękuję, już dziś przekażę Adresatowi

 

DZIĘKUJĘ!
JESTEŚ MIŁYM

GOŚCIEM
NASZEJ WITRYNY!